Latające Kamienie, czyli słów kilka o zdolnościach Tenshi Hinanawi
 Na wstępie chciałbym zaznaczyć, że poniższy tekst stanowi jedynie teorię i powstał jedynie ku uciesze autora.
To jest, na dole podpisanego.
Na wstępie chciałbym zaznaczyć, że poniższy tekst stanowi jedynie teorię i powstał jedynie ku uciesze autora.
To jest, na dole podpisanego.
A więc zastanawiało mnie co właściwie sprawia i jak racjonalnie można by wyjaśnić zdolności Tenshi do manipulacji skałami. Każdy, kto grał w TH 12.3 wie o czym mówię. Mnie zawsze „anioły”, kojarzyły się ze światłem. I jak by nie patrzeć światło stanowi klucz do wyjaśnienia fenomenu kamiennych pocisków, a zarazem, wyjaśnia zdolność wystrzeliwania czerwonych laserów. Tenshi posiada „zdolność manipulacji ziemią” – brzmi doniośle, czyż nie? Pewnie tak, i wielu ludziom takie wyjaśnienie wystarcza. Lubię przybliżyć sobie, istotę zjawiska ograniczając liczbę elementów „niesamowitych”, i uproszczając efekt do zjawiska które można symulować, czy też zbudować maszynę zdolną do osiągania takich efektów. I w tym konkretnym przypadku, światło spełnia w stopniu dość dobrym założenia.
Zanim przejdę do konkretów, akapit wprowadzenia. Który odpowiada na pytanie „Czym jest światło?”. O strukturze aktualnego poznania wszechrzeczy można książki pisać (i co nie powinno dziwić, jest to robione), więc na potrzeby tego tekstu, chcę się tu umówić z Tobą – czytelniku – na kilka założeń. Przyjmujemy, że wszechświat wypełnia pole elektromagnetyczne, ekscytacja tego pola to elektron, poruszające się elektrony spełniają założenia relatywistyczne. Przestrzeń wokół poruszającego się elektronu kurczy się, co opisuje skrócenie Lorenza Przez to pojawia się różnica między ładunkami spoczywającymi, a ładunkami w ruchu. Co obserwujemy jako pojawienie się dodatkowej siły kulombowskiej, nazywanej oddziaływaniem magnetycznym. (Tak nawiasem, magnetyzm jest zbędny w świetle unifikacji elektromagnetycznej, niemniej znacznie upraszcza równania). To tyle naszej umowy. Światło jest zaburzeniem tego pola. Z życia wiecie (dynamo przy rowerze), że zmienny wektor (wektor – myślę, że słowo to nie wymaga specjalnego wyjaśnienia?) magnetyczny – na przykład rotujący magnes sztabkowy – wytwarza zmienny wektor elektryczny. (Są one skierowane do siebie pod kątem prostym). Kiedy wektor elektryczny osiąga maksimum, wektor magnetyczny jest zerowy (cała energia w wektorze elektrycznym) i odwrotnie. I tak „pulsując” rozchodzące się zaburzenie tego pola to fala elektromagnetyczna, aka światło. Światło widzialne to jedynie niewielki wycinek światła jako takiego (O energii od 2.5467e-19 do 5.2275e-19 Joule’a na kwant). Co więcej oko ludzie wykrywa jedynie składowy wektor elektryczny, w odróżnieniu do ptaków które potrafią również widzieć wektor magnetyczny. Tutaj mała dygresja – Panie z PCB, nawiązują imionami do energii światła – pomarańczowy o najniższej energii, w japońskim zwany Chen. Indygo, ciemno niebieski o znacząco wyższej energii, po japońsku Ran. Oraz stojący blisko energetycznie przy Indygo, Fiolet – czyli Yukari. (Ilość energii przenoszonej przez kwant fioletu jest o 4.9786e-20 Joule’a większa niż Indygo – słownie około czterdzieści dziewięć tryliardowych części – zrozumiale: bardzo bardzo mało). Niemniej skoro istotę światła mamy za sobą, czas przejść do kolejnego akapitu.
Geologia Japonii i dlaczego metale oddziałują z polem magnetycznym.
Otóż żelazo posiada niesparowany spin.
Jak wiemy, przepływający prąd tworzy w pobliżu przewodnika, pole magnetyczne.
W atomach po orbitach "krążą" elektrony (słowo krążą zostało wzięte w cudzysłów ze względu na niedokładność pojęcia, które jednak jest poprawne dla przytoczonego niżej modelu):
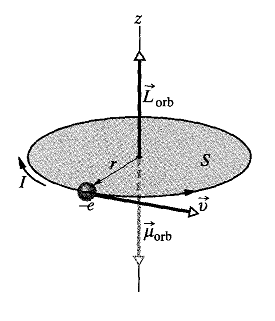
Elektron w tym przykładnie porusza się ze stałą prędkością v po kołowym torze o promieniu r, obejmującym powierzchnię S. Elektron ma orbitalny moment pędu Lorb i związany z nim orbitalny moment magnetyczny μorb. Prąd o natężeniu I, składający się z ładunków dodatnich i płynący zgodnie z ruchem wskazówek zegara, jest równoważny elektronowi poruszającemu się w kierunku przeciwnym. Co oznacza tyle, że każdy elektron w atomie posiada moment magnetyczny, jednak w przypadku większości substancji, moment magnetyczny równoważony jest zgodnie z zakazem Pauliego (W jednej przestrzeni orbitalnej, nie mogą istnieć dwa elektrony o tym samym spinie). Pary elektronów mają przeciwne spiny, niemniej w niektórych substancjach istnieją elektrony niesparowane, które tworzą moment magnetyczny. Kilka takich momentów w tym samym kierunku i mamy domenę magnetyczną, kilka domen w tym samym kierunku i mamy ferromagnetyk, który utrzyma ułożenie domen. Oto jak działa zewnętrzne pole magnetyczne na taką pętlę:
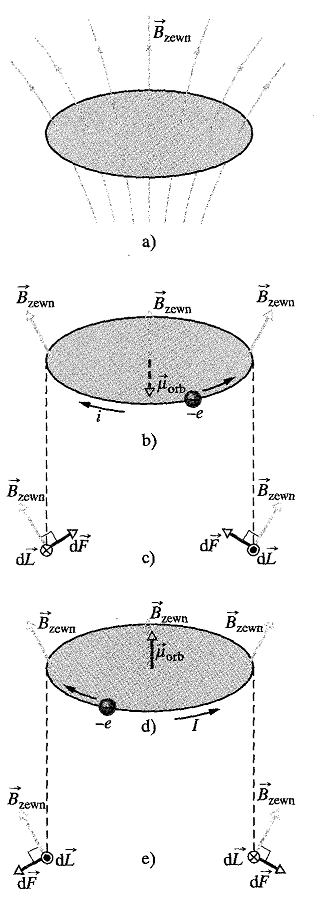
a) Model pętli z prądem dla elektronu krążącego w atomie, umieszczonym w niejednorodnym polu magnetycznym Bzew.
b) Ładunek -e porusza się przeciwnie do ruchu wskazówek zegara, więc umowny prąd o natężeniu I płynie zgodnie z ruchem wskazówek zegara.
c) Siły magnetyczne dF po lewej i prawej stronie widziane w płaszczyźnie pętli. Wypadkowa siła działająca na pętlę jest skierowana do góry.
d) Ładunek -e porusza się zgodnie z ruchem wskazówek zegara.
e) Wypadkowa sił działających na pętlę jest skierowana w dół.
Po tym lakonicznym omówieniu magnetyzmu żelaza, przejdźmy do geologii Japonii. Liczne, zwłaszcza na Sikoku i Kiusiu oraz w południowej części Honsiu, są skały metamorficzne i kompleksy ofiolitowe, które są fragmentami dawnego dna oceanicznego. Geologia Japonii obfituje też w skały pochodzenia wulkanicznego takie jak bazalty. Dało mi to do myślenia i niejako ugruntowało mnie w przekonaniu, że kamienie którymi miota Tenshi zawierają znaczące ilości Magnetytu, który występuje powszechnie w skałach magmowych (gabro, bazalt). Obecny jest również w skałach metamorficznych i osadowych. Dodatkowo w Japonii panowało wierzenie jakoby magnetyt łagodził ból, leczył schorzenia szyi, ramion oraz bezsenność.
Teraz należało by estymować masę, skał którymi miota Tenshi, średnią zawartość magnetytu w bazaltach japońskich, wzrost Tenshi i tym podobne.
Więc zacznijmy od najcięższego... czyli określenia wzrostu Tenshi.
Poniżej prezentuję przykładową estymację krok po kroku.
ZUN nigdy nie podał oficjalnego wzrostu postaci, niemniej wiemy że nadzoruje on prace grupy Twilight Frontier wydającej bijatyki.
Pierwszą moją myślą było przeliczenie wzrostu postaci z podanego przez ZUN’a rozmiaru piersi Bohaterek.
Niemniej w grze Tasofro obfite... ubrania, uniemożliwiają dokładnych pomiarów obwodu pod piersią i w piersi.
Więc należało dobrać inny obiekt, znajdujący się w tej samej płaszczyźnie co bohaterki.
Idealny okazał się wagon kolejowy którym posługuje się Yukari.
Prezentuję tutaj zdjęcie elektrycznego zespołu trakcyjnego, którym dostalibyście w rzeczywistości.
Przed państwem „営団3000系”!

Oraz dla porównania jego odpowiednik z gry.

Oraz specyfikacja techniczna naszego elementu odniesienia:
Material wagonu: Stal Nierdzewna
Długość wagonu: 18,000 mm
Szerokość wagonu: 2,790 mm
Wysokość wagonu: 3,995 mm
Drzwi: Trzy pary na stronę
Prędkość maksymalna: 100 km/h
Przyspieszenie: 4.0 km/h/s
Hamowanie: 4.0 km/h/s (service) 5.0 km/h/s (emergency)
System zasilania: 1,500 V DC
Metoda poboru energii: Napowietrzna linia energetyczna
Systemy bezpieczeństwa: Tobu ATS, Tokyu ATS, WS-ATC (ATO)
Rozstaw torów: 1,067 mm (3 ft 6 in)
Nas interesuje głównie wysokość, jako że jest to wymiar nie zniekształcony perspektywicznie na posiadanym rysunku.
Zwykle wysokość wagonu podaje się od główki szyny do dachu i to też przyjmę za odniesienie.
Mierząc wysokość wagonu przy pomocy windowsowskiego Painta (nie potrzebne jest tu bardziej wyszukane narzędzie) otrzymałem wynik 176 pikseli.
Więc wiemy że 176 pikseli odpowiada 3995 mm.
Natomiast mój model przykładowy, mierzony od pięt do czubka głowy posiada 96 pikseli (+- 3 piksele niepewności pomiaru) wzrostu.

Stosując uroczo prostą arytmetykę, otrzymujemy odpowiedź: Ran Yakumo ma tutaj 2179 mm co odpowiada wzrostowi ~2 metry 18 centymetrów (y = ax + b – funkcja liniowa dla której współczynnik kierunkowy wynosi około 22,6988(63), prosta przecina układ kartezjański w punkcie 0 (b=0), x to wzrost w pikselach, a y to wzrost w milimetrach). A ogon ma długość około 1 metra. (Powodzenia Cosplayerki ^ ^). W identyczny sposób określiłem wzrost Tenshi na 1 metr 88 centymetrów posługując się poniższym modelem.

Dla porównania do klasycznych loli – Suika otrzymała wynik 1 metr 67 centymetrów. Art pomiaru:

Wzrost za nami.
Teraz należy wyznaczyć objętość i masę głazów.
Wybrałem te najbardziej kuliste aby uprościc obliczenia (Oczywiście jeśli – drogi Czytelniku – odtarłeś, do tego punktu i chcesz znać wielkości i masy wszystkich pocisków, nie ma problemu.
Daj znać a napiszę aneks uzupełniajacy do tego tekstu).
Wzór na objętość kuli powinien znać każdy – niemniej podaję – Objętość kuli o promieniu r wynosi
Więc nasz kamyczek:

Przybliżony modelem kuli, posiada średnicę 1 metra 11 cm. Czyli objętość 0,716 m³. Średnia gęstość magnetytu to Więc masa tego głazu to 3723,200 kg. Huhu... ponad trzy i pół tony... no to jest 5 fiatów 126p...a Tenshi może obracać trzema takimi na raz. Przejdźmy teraz do zadania sobie pytania jakiej energii Tenshi potrzebuje by unieść taki kamień w jednorodnym polu grawitacyjnym o przyspieszeniu Jako że obliczenie siły oddziaływania między dwoma biegunami magnetycznymi, nie jest sprawą prostą, zakładam że Tenshi wytwarza równomierne dipolowe (zgodnie z prawami Maxwella – iloczyn gradientu pola oraz indukcji magnetycznej jest równy zero. Lub jak kto woli calka powierzchniowa po obrysie zamkniętym, dla indukcji magnetycznej jest równa zero. Innymisłowy pole magnetyczne jest bezzźródłowe. Jeszcze prościej – nie istnieją monopole magnetyczne. Magnes ma zawsze dwa bieguny. I chuj.) pole magnetyczne w kształcie czaszy nad powierzchnią kamienia, tworząc swoistą „miskę magnetyczną”. Więc dane:
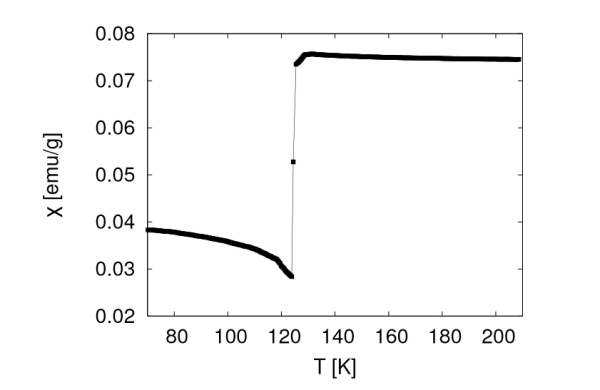
Zależność temperaturowa podatności magnetycznej. Wg [Kąkol et al., 2000]
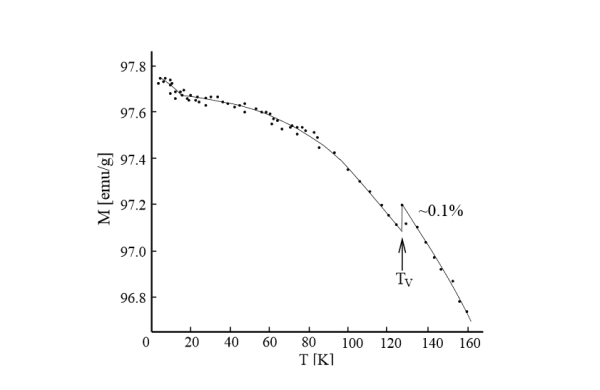
Z wzoru mówiącego o zależności magnetyzacji od iloczynu natężenia pola i podatności magnetycznej , na podstawie danych wykresów obliczamy natężenie pola H. Równanie na Hᴛ które stanowi natężenie pola magnetycznego które musi wytworzyć Tenshi aby unieśc taką skałę ma postać: Siła z jaką oddziaływuje kamień to F𝐹=𝑚ma. Podstawiajac do wzoru otrzymujemy I takie właśnie natężenie pola jest konieczne do możlwości swobodnego operowania tą skałą. Stosując tą informację można zaprojektowac cewkę potrzebną do operacji takim obiektem. Moc jaką wkłada Tenshi w wytworzenie takiego pola jest zapisana wzorem Gdzie Rᴘ to opór elektryczny powietrza (około , B obliczona gęstość strumienia magnetycznego, l to droga magnetyczna, n liczba okręgów zataczanych przez elektrony, μ to zaś przenikalność magnetyczna środka (powietrza) w Henrach na metr. Podstawiając dane do wzoru (za l przyjmuję – pole „na styk”) otrzymujemy moc Tenshi włożoną w wytworzenie takiego pola poprzez ruch elektronów w ośrodku jakim jest powietrze, bez uwzględnienia (istotnego – acz nieobserwowanego w grze) wpływu jonizacji na równą 1888687875 W, czyli około 1,889 GW – Tyle co mała elektrownia nuklearna (Gdyby użyć miedzi, to jeden pierścień wystarczyłby i zużywał 18 watów – inna sprawa, że takie natężenie miedź wytrzymała by kilka części sekundy – dlatego stosuje się więcej zwojów (oraz rdzenie), dzięki czemu można obniżyć natężenie, przy 5000 jest już ono całkiem znośne - na poziomie 4 A). Utrzymanie takiego przepływu przez 2 sekundy, wymagało by energii równej anihilacji 0,045 miligrama materii. Jednak zużycie to zależy w tej sytuacji, od ilości pierścieni elektronowych, przy 10 000 moc spada już do około 1,8 kW. Odpowiedź na pytanie o moc jaką Tenshi wykorzystuje, można więc zmienić na pytanie – Iloma pierścieniami elektronowymi może jednocześnie się posługiwać? A to – drogi czytelniku - pytanie personalne, a nie fizyczne. Nadanie kamieniowi energii potencjalnej będzie nakładem energetycznym który dodatkowo, będize musiała ponieść bohaterka (Jest on co prawda znikomy – w porównaniu do poprzedniej wartości - ale zawsze). Zgodnie z równaniem Eᴘ = mgh. Co w przypadku tego konkretnego głazu podniesionego na wysokość 1 metra wyniesie Eᴘ = 36524,592 J = 36,524 kJ. Czyli podniesienie takiego kamienia wymaga bezpośrednigu zużycia około 8,72 kcal energii. Taka ilość energii zawarta jest w około jednym gramie tłuszczu.
Tu wypada nadmienić, że dorosły męszczyzna potrzebuje spożyć 2800 kcal. Jak widać praca fizyczna zabiera o wiele mniej energii niż przemiany chemiczne czy wydzielanie ciepła. Jeśli zatem Tenshi manipuluje swobodnie polem elektromagnetycznym, model ten będzie również trafny w opisie wystrzału czerwonym laserem. Niemniej to temat na inny raz.
Archi
 Legacy of Lunatic Kingdom
Legacy of Lunatic Kingdom

